1. First integral of a Pfaffian equation

$F$ is a first integral of the Pfaffian equation $\omega\equiv 0$ if there exists $\mu$ such that $F$ is a primitive of $\mu \omega$:

The function $\mu$ is called integrating factor.

It is said that the 1-form is a Frobenius integrable 1-form.

This terminology is taken from Maple Help page, for the command FirstIntegrals:

Observe that the characterization $\operatorname{df} \wedge \theta^{1} \wedge \theta^{2} \wedge \cdots \wedge \theta^{p}=0$ let us try to find the first integral without looking for the integrating factor.

2. First integral of a vector field

$F$ is a first integral of a vector field $X$ if $X(F)=0$. The meaning is that the flow of $X$ is contained in hypersurfaces $F=constant$.

Observe that a first integral of the vector field is a solution of the PDE

of which is its characteristic equation.

First integrals of a vector field are also called their invariants, and they serve to straighten the vector field: see canonical form of a regular vector field

3.a. First integral of a first order ODE system

(and therefore of a $m$th-order ODE system)

It is a first integral $F$ of the vector field $A$ associated to the system, i.e.,

Solution curves (or their prolongations, if we are in higher order) are contained in $F=constant$.

This is generalized to any system of DEs with the notion of conservation law.

3.b. First integal of an $m$th-order ODE

Given an ODE $\Delta$, we call a first integral of $\Delta$ to any smooth function $F\in J^m$ (the jet bundle) such that

for a never vanishing smooth function $\mu$ called integrating factor.

Equivalence with 3.a.

This definition is equivalent to the previous one, since if $A(F)=0$ then

and so

And conversely, if $D_x(F)=\mu(u_2-\phi)$

and therefore $F_{u_1}=\mu$ and so

$$A(F)=F_x+F_u u_1+F_{u_1}\phi=\mu u_2-\mu \phi-F_{u_1}u_2+F_{u_1}\phi=0.$$

Relation to definition 1 above

The ODE $u_2-\phi(x,u,u_1)$ can be though as the 1-form

In order 1, this 1-form is the only thing we have regarding the ODE, there is no more information. In higher order we have more data: the Cartan distribution. With this preliminaries we can assure:

Proposition

There exist a pair $(F,\mu)$ such that $D_x(F)=\mu \Delta$ if and only if $dF=\mu \alpha$ for certain 1-form $\alpha \equiv du_1-\phi dx$ mod $\mathcal{E}$, i.e. $\alpha=du_1-\phi dx+c\theta_0$.

This result can be stated for any order $m$.

Proof

[xournal 126]

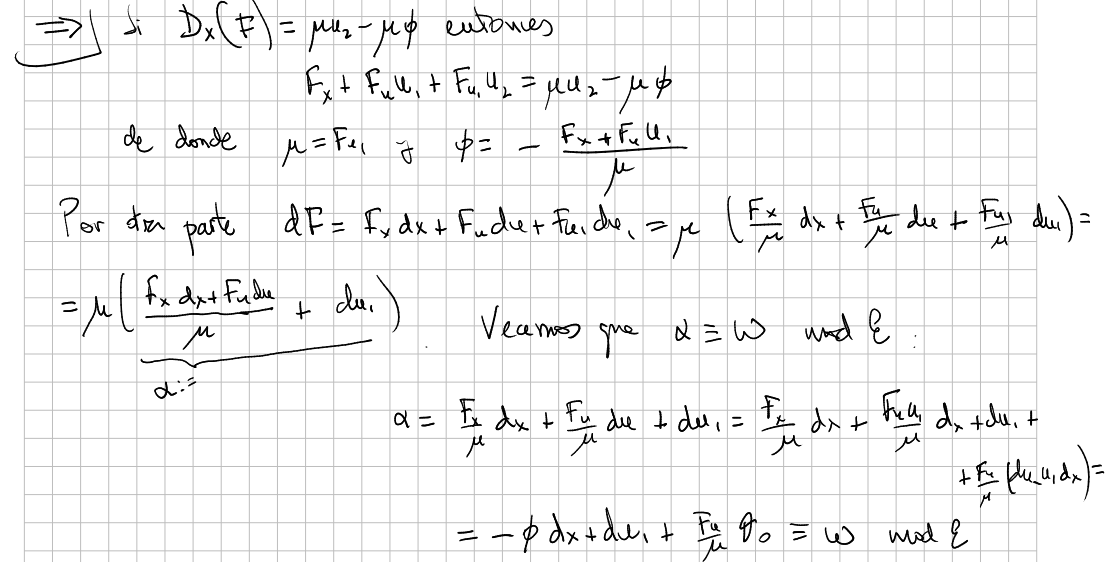
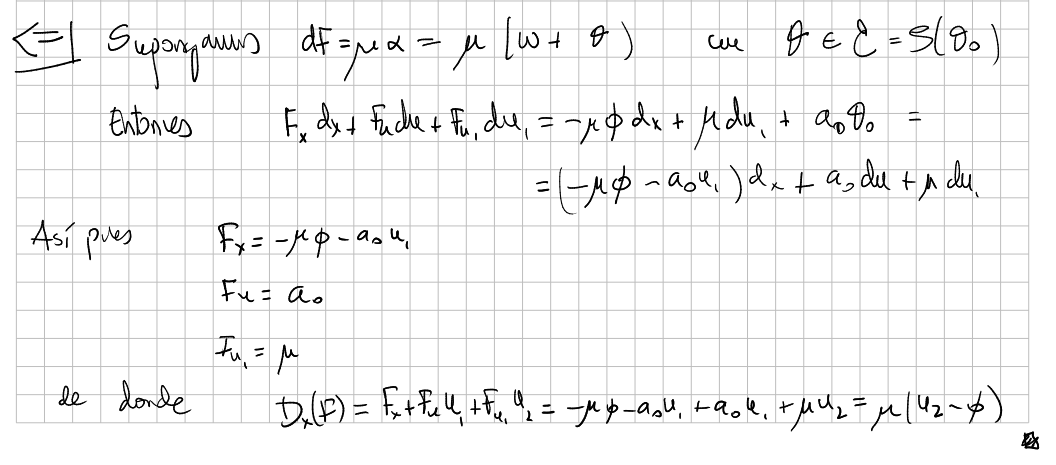
4. First integral of a distribution

Given a distribution $D$ on a manifold $M$, a function $h\in \mathcal{C}^{\infty}(M)$ is called a first integral of $D$ if every integral submanifold of $D$ is contained in a level surface of $h$, or equivalently if $V(h)=0$ for any $V\in D$. It is coherent with this definition.

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es